FID: Fréchet Inception Distance
Quoth Wikipedia:
The Fréchet inception distance (FID) is a metric used to assess the quality of images created by a generative model, like a generative adversarial network (GAN). Unlike the earlier inception score (IS), which evaluates only the distribution of generated images, the FID compares the distribution of generated images with the distribution of real images that were used to train the generator.
The FID metric is the squared Wasserstein metric between two multidimensional Gaussian distributions: \(\mathcal{N}(\mu,\Sigma) \) , the distribution of some neural network features of the images generated by the GAN and \( \mathcal{N}(\mu_{w},\Sigma_{w}) \) the distribution of the same neural network features from the “world” or real images used to train the GAN. As a neural network the Inception v3 trained on the ImageNet is commonly used. As a result, it can be computed from the mean and the covariance of the activations when the synthesized and real images are fed into the Inception network as:
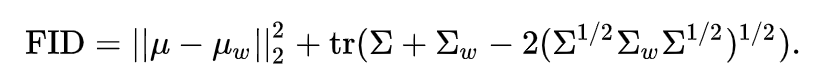
In summary
FID score is the distance between the distribution of the activations for some deep layers in a classifier, when comparing a sample of test images and one of generated images. If activation distributions are similar, we can conclude the underlying image distributions are also alike.
The Wasserstein metric is computed as the distance between the means plus a term that takes covariance matrices into account. This metric is used for computing the distance between two distributions, similar to KL-Divergence (I wonder how well they correlate?).
Wasserstein vs Kullback-Leibler
“When considering the advantages of Wasserstein metric compared to KL divergence, then the most obvious one is that W is a metric whereas KL divergence is not, since KL is not symmetric, and does not satisfy the triangle inequality.” Source: Mathstack